Gravity & space-time

An exploration

Einstein stated that when calculating gravitational attraction at astronomical distances the mass could be assumed to be a point source. Physics texts consistently use this assumption when calculating gravitational attraction with two objects at any distance.

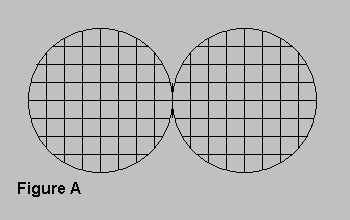
I was curious if there would be a difference in calculated gravitational attraction if the mass was distributed and the distance quite close. Using the example of two spheres touching one another, I let the computer divided the spheres into cubes, and calculate the attraction between each cube and every cube in the companion sphere. See figure A below.

When totaled, the difference is exactly twice what the gravitational attraction would be if calculated using the center of each sphere as a point mass. Running the program with other uniform geometric shapes the same results. Furthermore, it makes no difference if the objects are considered to be two-dimensional or three-dimensional.

The difference becomes negligible as the spheres are moved apart beyond one diameter, due to the distance square law.

After discovering this, I wondered how much mass at a very close distance it would take to nullify the Earth's gravitational pull assuming a point source. If 38 tons of mass could be squeezed into a pinpoint, it should levitate an object if located a millimeter above it.

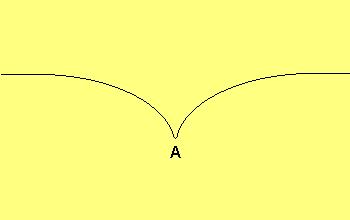
Einstein described the stretch in space-time (gravity) caused by the presence of matter as being similar to a heavy object placed on a rubber sheet ('A' above).

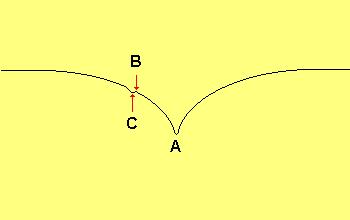
If the object we want to "levitate" is located at point 'B' all we have to do is create a space-time distortion "above" the object at 'C'. If the distortion could be moved as object 'B' rose, object 'B' would follow, much as a surfer riding a wave.